The ratio of the risk associated with a portfolio construction to the gross risk:
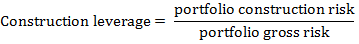
A portfolio’s construction risk refers to the risk of the portfolio given the actual diversification or hedging undertaken, while the gross risk is typically based on the assumption that there were no diversification or hedging benefits. This leverage arises because the risk of a portfolio is not necessarily equal to the sum of the risks of component positions. In non-diversified portfolios, the portfolio risk would equal the sum of the risks of component positions. In this case, the correlation among all the individual positions would be 1.0, implying that the portfolio is virtually made up of one position. Successful diversification can have the effect of reducing risk without negatively impacting returns.
The following example demonstrates how conceptually and practically the construction leverage works:
| Portfolio 1 | Construction Risk | Portfolio 2 | Construction Risk |
|---|---|---|---|
| Long Retailer A | 3.5% | Long Retailer A | 1% |
| Long Retailer B | Short Retailer B |
In this example, construction risk is measured as the monthly standard deviation. Both portfolios assign equal weights to each company. However, portfolio (1) is long both companies, while portfolio (2) is long one and short the other. The construction risk in the portfolio with opposite positions is lower than it in the portfolio which is long throughout. In other words, as portfolio (1) is not diversified, there is a noticeable amount of construction risk associated therewith. This risk gives rise to construction leverage.





Comments