A classification of option greeks that relate to, or are based on, delta. Examples include delta (for calls and puts), spot delta and futures delta, DdeltaDvol, DvegaDspot, DvannaDvol, DdeltaDtime, elasticity (call elasticity, put elasticity), etc. Delta, by definition, is the option’s sensitivity to “small” changes in the price of its underlying asset. In other words, delta is the connection between an option’s price (option value) and its underlying price.
For a call, delta is given by:
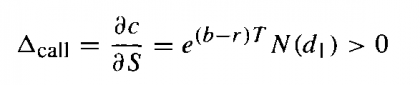
Where: c is the call option’s price, δc is the change in the option price, S is the underlying price, δS is the change in the underlying price, T is time to expiration, r is the risk-free rate, and b is cost of carry.
N(d1) is the factor by which the present value of contingent receipt of the underlying asset exceeds the current underlying price. In other words, N(d1) is the present value of receiving the underlying if and only if the option finishes in the money.
And for a put, delta is calculated as follows:
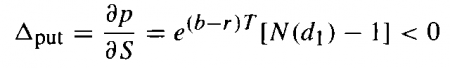
Where: p is the put’s price and δp is the change in the put’s price.
Delta greeks are a subset of Black-Scholes-Merton Greeks.



