An option leverage that measures the sensitivity of a put option’s price to changes in the underlying price. In other words, it is the percentage by which a put option’s price changes for a 1% change in the underlying price. Typically the leverage of an option is related to its delta, and for a long put option it equals the negative value of delta multiplied by the ratio of the underlying price to the option price. The following formula is used in calculating the leverage of a put:
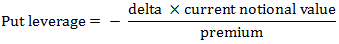
Using the Black-Scholes model, put leverage can be expressed as follows:

where: S is the underlying price, P is the option’s price (premium), N(d1) is the cumulative standard normal distribution for the value d1 (which itself is a numerical parameter that depends on the model’s inputs, q is the continuously compounded risk-free interest rate per year, and T is the option’s time to expiration.
The numerical parameter d1 is usually calculated using the following formula:
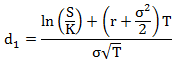
where: K is the strike price, r is the risk-free interest rate, σ is the underlying’s volatility, and T is time to expiration.