One of the most popular proxies of credit spread is the CDS-bond basis, which captures the excess of the CDS spread over the asset swap spread for a given company (reference entity). The probability of default can be estimated in an approximate way using the concept of hazard rate. By definition, it is:

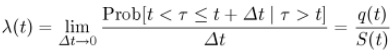
Where h is the hazard rate (default intensity) per annum, s is the spread of risky bond yield over risk-free rate, and R is the expected recovery rate.

We resort to the bootstrapping of hazard rates in order to infer an approximate value of the credit spread for a specific maturity. For example, suppose the CDS spreads for 3-year, 5-year, and 10-year corporate bonds are 65, 75, and 120 basis points, respectively, and that the expected recovery rate is 65%. Then, the average hazard rate over 3-year, 5-year, and 10-year maturities is:

3-year h= 0.0065/(1-0.65) = 0.0186

5-year h= 0.0075/(1-0.65) = 0.0214

10-year h= 0.0120/(1-0.65)= 0.0343

The hazard rate between year 3 and year 5 can be bootstrapped using the following formula:

By plugging in the numbers for year 3 and year 5, the average hazard rate between these two years is:

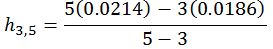
h_3,5 = 0.0256

and between year 5 and year 10, it is:

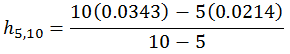
h_5,10= 0.0472

This calculation method works well when the reference bond is selling for close to its face value (par value). When the bond’s market price is not close to par, another method (based on the expected loss from defaults) is used instead.