A statistical test in which the critical area of a distribution (e.g., normal distribution) is either above or under a certain value (significance level). The test is appropriate if the estimated value departs, or is assumed to depart, from the reference value in only one direction, left or right. If a mean is x, this test helps determine (the probability) if a set of results is more than x or less than x.

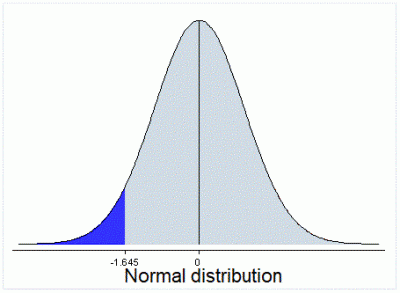
A left-tailed test is applied when the alternative hypothesis assumes that the true value of the parameter in the null hypothesis is lower than what the null hypothesis sets forth. In the below graph, the shaded area is 0.05 of the total area below the curve:

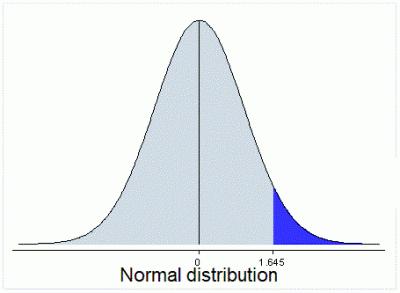
A right-tailed test is used when the alternative hypothesis assumes that the true value of the parameter in the null hypothesis is larger than the value specified in the null hypothesis.

In the below graph, the shaded area is 0.050 of the total area above the curve:

For a significance level of .05, a one-tailed test examines the statistical significance in the one direction of interest. In other words, a significance level of 0.05 would lie only in one tail of the distribution of the test statistic. Here, the test focuses on the possibility of a one-direction relationship, while completely disregarding the possibility of a relationship in the other direction.