A risk-adjusted return measure that quantifies the return generated by a hedge fund for each unit of risk it takes. This ratio is based on a popular statistical tool: standard deviation. In calculating Sharpe ratio, a fund’s excess return over cash is divided by the fund’s standard deviation as illustrated below:

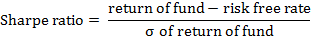
A risk-adjusted ratio that uses downward deviation (instead of standard deviation) as a measure of risk. It is calculated by dividing a hedge fund’s excess return over cash (i.e., risk-free return) by the fund’s downward deviation. In this sense, Sortino ratio fine-tunes Sharpe ratio as it doesn’t take into account the overall volatility of a fund. Instead it reflects the adverse volatility arising from returns lower than a minimum acceptable return. The following formula illustrates the concept of Sortino ratio:

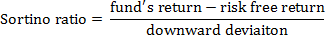
Alternatively, it can be given by the following equation:

The downside or downward deviation is calculated as follows:

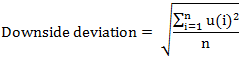
where u(i) = 0 if a fund’s return r(i) is higher than, or equal to, the minimal acceptable return (MAR) or u(i) = r(i) – MAR if a fund’s return is lower than the minimal acceptable return.

This measure of risk is almost ineffective when used to assess funds with substantially low levels of volatility. Furthermore, as it solely focuses on downward volatility, Sortino ratio could be inferior to Sharpe ratio in cases where both upward and downward volatility contribute to a fund’s risk. That is why this measure particularly suits investments with high volatility.