A risk-adjusted return measure that quantifies the return generated by a hedge fund for each unit of risk it takes. This ratio is based on a popular statistical tool: standard deviation. In calculating Sharpe ratio, a fund’s excess return over cash is divided by the fund’s standard deviation as illustrated below:

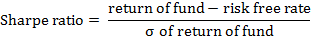
The higher this ratio, the higher the fund’s return is. High ratios indicate that return is sufficient to compensate for the risk taken (i.e., volatility of return). Characteristically, standard deviation is a measure of total risk (i.e., that of entire portfolios rather than individual investments). The Treynor ratio, for example, uses beta as a measure of risk. In the realm of hedge funds, however, betas are particularly irrelevant. Instead, the Sharpe ratio reasonably fits into measuring the performance of a fund or a set of funds.

The use of standard deviation as a measure of risk associated with hedge funds is, nevertheless, a subject of debate especially that it helps conceal occasional large losses under the mask of one final figure.