In essence, beta is a measure of how a stock’s volatility changes in relation to the overall market. An option’s beta is the covariance of the option’s return with the market return divided by the variance of the market return. An option’s beta can be computed using the concept of elasticity. In other words, the option’s possible returns are related to the underlying’s possible returns. This brings to mind the capital asset pricing model (CAPM): if asset prices follow geometric Brownian motions, the continuous-time CAPM holds. As such, the expected return on a given asset, g, will satisfy the intertemporal CAPM equation:

where rf is the risk-free rate, rm is the expected return on the market portfolio, and βS is the beta of the asset. Since the CAPM applies to all risky assets, it also applies to options. The expected rate of return of a call option written on the asset may be determined by first figuring out its beta. The beta of a call is given by Black and Scholes (1973):

While the beta of a put is:
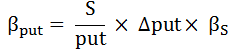
The expected rate of return of a call option on the asset may be expressed as:
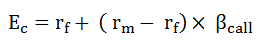
In this sense, the expected return on a beta neutral option strategy should be equal to the risk-free rate.



