An option pricing model that is used to value European futures options. This model was first developed by Fischer Black in 1976, and in which the futures price was assumed to follow a lognormal process. A futures option is similar to an option on a stock as it provides its holder with the right to buy or sell the underlying at the exercise price of the option. However, a futures option entitles its holder, upon exercise, to acquire a long or short futures position with a futures price equal to the exercise price of the option. In this sense, a futures option doesn’t end up with cash exchange on exercise.

Black derived the valuation formula for a European call option on futures contracts by assuming futures prices are lognormally distributed and that it is possible to set up a riskless hedge between the European call and its underlying futures contract. As a result, the value of a European call can be given by the following equation:

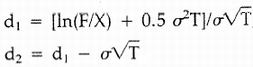
σ is the volatility of the futures price, X the exercise price, T time to expiration. F denotes the current futures price, while r is the riskless rate of interest. N₁(d₁) is the probability that a unit normally distributed random variable x will be less than, or equal to, d.

The above equation, notwithstanding, may actually underestimate the value of an American call option on a futures contract (American futures call option) because it is unable to take into consideration the potential advantage of exercising the option any time before its expiration date. In pricing American futures options, the so-called compound value approach is used (see American futures options pricing).