In order to price a convertible bond using the Black-Scholes model, the following two steps would need to be taken:
- calculate the investment value of the bond.
- make adjustments to the investment value to account for the effect of early conversion on the maturity of the bond and the term of the warrant and also any potential losses in accrued interest due to a forced conversion.
Suppose a convertible bond has the following features:
| Maturity date | 25 January 2017 |
| Par value | $1,000 |
| Issue size | $150 million |
| Term | 5 years |
| Call protection | 5 years |
| Coupon | 6% |
| Coupon payment frequency | 6 months |
| Issue price | 100% |
| Redemption price | 100% |
| Underlying stock price at issue | $75 |
| Conversion price | $100 |
| Conversion premium at launch | 25% |
| Denomination per bond | $1,000 |
| Conversion ratio (=denomination per bond/conversion price) | 10 |
| 5-year risk-free rate | 5.5% |
| Credit spread | 3% |
| Existing shares outstanding | 10 million |
| Shares created by the convertible | 1 million |
| Dilution (=shares created/existing shares outstanding) | 10% (=1/10) |
| Stock price volatility | 35% |
| Dividends | nil |
Calculating the investment value of the bond requires determining the periodical coupon: C= 6%x1000/2 = 30, and the periodical discount rate: YTM= (risk-free rate + credit spread)/2 = (5.5% + 3%)/2 = 8.5%/2= 4.25%. Now we plug in these figures into the following formula:
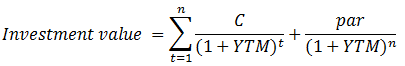
It follows that:
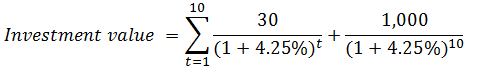
The following table enlists all cash flows generated by the bond over its life:
| Period (t) | Cash flow | Present value cash flow |
|---|---|---|
| 0.5 | $30 | $28.77 |
| 1.0 | $30 | $27.60 |
| 1.5 | $30 | $26.47 |
| 2.0 | $30 | $25.39 |
| 2.5 | $30 | $24.36 |
| 3.0 | $30 | $23.37 |
| 3.5 | $30 | $22.41 |
| 4.0 | $30 | $21.50 |
| 4.5 | $30 | $20.62 |
| 5.0 | $1030 | $679.31 |
| Total | $899.80 |
Adjusted exercise price= investment value/conversion ratio = $899.80/10= $89.98
To calculate the value of a call warrant, we first figure out d1 and d2:
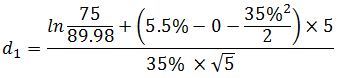
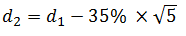
d1= -0.2726, d2= -0.2726 – 0.7826 = – 1.0552
value of a call warrant = N(-0.2726) x $75 – N(- 1.0552) x $89.98. e-0.055×5 = $19.48
value of the call component in each bond = value of the call warrant x conversion ratio = $19.48 x 10= $194.8
value of the warrant = [1/(1+λ] x value of the call component = (1/1.1) x $194.8 = $177.09
Therefore, the theoretical value of the convertible bond is:
- convertible bond value = investment value + value of the embedded call = $899.80 + $194.8 = $1,094.6
- Taking into account the effect of dilution, convertible bond value = $899.80 + $177.09 = $1,076.9
This convertible bond is worth $1,094.6 before dilution, and $1,076.9 after dilution.
Comments
Etienne d'Ouala
April 15, 2022 at 3:57 amGreat post. Are you sure your d1 is correct ? should not it be + vol^2 /2 ?
Fincyclopedia
April 17, 2022 at 7:36 amThank you, Etienne. Correct (Here is Black-Scholes: https://fincyclopedia.net/derivatives/b/black-scholes-equation). Initially, it seems to be a typo. But will do calculations to see whether it did impact all the chain of calculations or not.