A convertible bond can be viewed as a combination of a straight bond with a call option on the underlying stock. The call option embedded in a convertible bond differs from an ordinary call option in that it (the embedded option) is actually a warrant which results in dilution on exercise, and that it involves conversion by the exchange of a bond for stock not by paying cash. Calculating the price of a convertible bond starts with determining its investment value, and then making adjustments thereto. The investment value of a bond is the sum of the present values of the expected future cash flows:
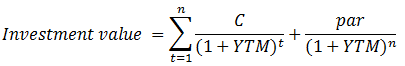
Where: C is the coupon rate, par is the par value of the bond, YTM is the yield to maturity (the discount rate), and n is the number of payment periods to maturity. The exercise price (i.e., the conversion price) will need to be adjusted using the following formula:
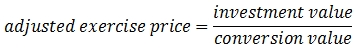
Then, we calculate the price of one embedded call warrant using the Black-Scholes formula:
Value of a call warrant = (warrant delta x stock price) – (borrowed amount)
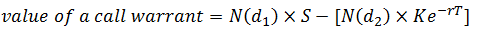
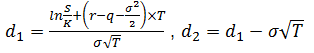
The borrowed amount represents a leveraged investment in the underlying stock. N(d) is the cumulative normal probability density function, q is the annualized continuous dividend yield, K is the exercise price of the option, r is the risk free rate of interest, T is the time to the exercise date in years, S is the current stock price, and σ is the volatility of the stock price.
value of embedded call per bond = call warrant price x conversion ratio
To adjust for dilution, the value of a warrant is calculated using the following formula (assuming each warrant can be exercised into one share) :
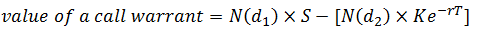
A practical example would illustrate just how this model does work (read more: pricing a convertible bond using the Black-Scholes model: an example).







