Most bonds pay coupons to the holder on a periodical basis, whilst the bond’s par value (principal) is paid back to the holder at maturity. Theoretically, the price of a bond is the present value of all the cash flows that the holder receives. Sometimes, the same discount rate is applied to all the cash flows generated by a bond. However, it is practically more accurate to use a different zero rate for each cash flow. The following example illustrates this.
Suppose Treasury zero rates (continuously compounded) are given in this table:
| Maturity (years) | Zero rate (%) |
|---|---|
| 0.5 | 4.0 |
| 1.0 | 4.8 |
| 1.5 | 5.5 |
| 2.0 | 6.0 |
The Treasury bond has a 2-year maturity and a par value of $100. Its coupons are based on a 5% rate per annum, paid semiannually. Therefore, each coupon is worth $2.5, and it would be discounted over the life of the bond using the zero rates shown in the table. If p, c, t, r, and f denote the bond price, coupon payment, coupon maturity, zero rate, and bond’s face value respectively, then:
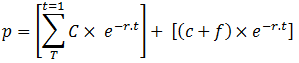
p = 2.5. e – 0.04×0.5 + 2.5. e – 0.048×1.0 + 2.5. e – 0.055×1.5 + 102.5. e – 0.06×2.0
= 2.450 + 2.382 + 2.302 + 90.909
= 98.04







