A variance swap is a forward contract on annualized variance which pays out at expiration an amount equal to:

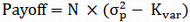
is the realized variance of the underlying (quoted in annualized terms) over the swap tenor, K_var is the delivery price for variance, and N is the notional amount of the swap in dollars per annualized volatility point squared. The implied volatility (particularly the ATM volatility) is the chief driver of the mark-to-market (MTM) value of a variance swap, be it a spot or a forward start swap. This value is also influenced by the skew corresponding to the variance swap’s maturity. In this sense, the realized volatility has no impact on the variance swap insofar as the swap has not begun.

However, with the passage of time, the swap diverts from its initial zero value. In order to re-evaluate the market value of the variance swap, let’s use the following notations: T for the swap’s maturity and ΔT for the time shift between inception and re-evaluation. During the time shift, the implied volatility could have changed due to an evolving realized variance (actually, the underlying price must have experienced additional variance). The market value of the variance swap is no longer zero after any time interval. The new value will be associated with a specific payoff which, per se, can be broken down into two components: (1) the realized variance over the time shift and (2) a new spot start variance swap value over the remaining time to maturity.

At this point, the mark-to-market value can be calculated using the following formula:

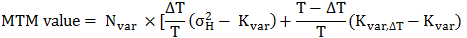
Where:

is the realized variance calculated for the interval ΔT (this figure is a historical variance that will be weighed against the strike price of the variance swap:K_var).

If the realized standard deviation (historical) is larger than the strike standard deviation, the variance swap will be of positive value to the benefit of the holder.

The value of a new spot start variance swap with the original strike K_var is also captured by the above formula, though it is valued against a different volatility surface. Given this new volatility surface, the new fair value strike will be K_var,ΔT. This equation demonstrates how the sensitivity of the value of the variance swap decreases in linear fashion with the passage of time.