A measure of a bond’s convexity which takes into account the convexity of options embedded within the bond. It captures the curvature of the price/yield relationship observed in bonds. Low values mean the relationship is near to linearity (a change in the price leads to a proportional change in the yield). The effective convexity may vary from the negative to the positive, depending on the yield’s amount and the time to call or time to put. For example, for immediately callable bonds, the price/yield relationship features positive convexity at high yields and negative convexity at low yields. The effective convexity, in contrast with modified convexity, assumes that the cash flows of a bond change when yields change. It is the second derivative of the effective duration.
Mathematically, the effective convexity is given by:
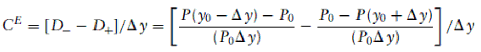
where:
D- is effective duration when the yield decreases
D+ is effective duration when the yield increases
P0 is the price of the bond at time 0
P1 is the price of the bond at time 1
Δy is the change in the yield
If there are no options embedded within a bond, the effective convexity is equal to normal convexity.
The effective convexity is also known as option-adjusted convexity.


