Essentially, a floor is a strip of put options on forward interest rates. Therefore, a floorlet is a put option on a forward interest rate:

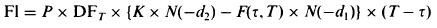
where: Fl is the floorlet’s price, P is the principal amount of the put option, DF_T is the discount factor at time T, F(t, T) is the forward interest rate between time t and time T, K is the strike price of the put option (%), and N(-d₂), N(-d₁) are the cumulative unit probability distribution functions for a standard normal distribution:

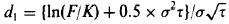
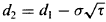
where: σ is the volatility of the forward interest rate

The payout of the floorlet is: max [0, K-L] x (T-t) x P
where: L is the fixing of forward interest rate that is observed at time t (it is a percentage rate %).

For an example, see: using the Black-Scholes Model to price floorlets- an example.