In a newly issued swap, the fixed rate equals the swap rate. When principal amounts are added to both legs on the final payment date, the swap is rendered into an exchange of a fixed-rate bond for a floating-rate bond. It follows that swap rates define par yield bonds and can be used to bootstrap the LIBOR zero curve (or LIBOR/ swap zero curve).
By convention, derivatives traders are most likely to use LIBOR rates as proxies for riskless reference rates when pricing derivatives. However, LIBOR is only observable for maturities of 1 year and below. Thus, longer maturities require a different calculation tool. The LIBOR zero curve can be extended beyond one year using Eurodollar futures (actually they are used to produce a 2- to 5-year LIBOR zero curve). For longer maturities, traders mainly use swap rates. Swap rates are rates paid by the fixed rate payer in exchange for receiving three-month LIBOR. Swaps are typically seen as consisting of two bonds, each on a different leg.
The value of a newly issued floating-rate bond that pays 6-month LIBOR is always equal to par when the LIBOR/swap zero curve is used for discounting (i.e., if the bond pays LIBOR and it is discounted at LIBOR then it fairly sells at par). As the fixed rate equals the swap rate, for a newly concluded swap, the floating rate equal is the notional principal amount (NPA). It follows that the fixed rate equals the swap’s NPA. Swap rates, as such, define a set of par yield bonds. The bootstrap method can be used to extend the LIBOR/swap rate curve beyond short maturities. The following example illustrates how this can actually be done:
Consider the following set of LIBOR/ swap zero rates:
| Period | Rate (c.c) |
| 6 months | 4.5% |
| 12 months | 4.9% |
| 18 months | 5.2% |
Suppose the 2-year swap rate is 5.5% (that means, a bond with a principal of $100 and a semiannual coupon of 5.5% per annum is selling for par). Consequently, if R is the 2-year zero rate, then:
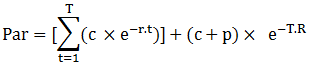
100 = 2.75 e-0.045 x 0.5 + 2.75 e-0.049 x 1 + 2.75 e-0.052 x 1.5 + 102.75 e-2R
Solving this equation, R= 5.47%.



