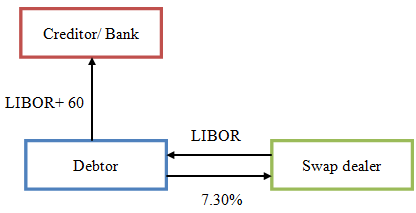
A fixed-rate loan can be synthetically constructed using interest rate swaps. A debtor with a floating-rate loan can convert his loan into a fixed-rate loan (in order to hedge against foreseen increases in interest rates) by entering the swap market to lock in his interest expense. This is usually done by concluding an interest rate swap in which the debtor pays fixed and receives floating. The following example illustrates how such a loan can be synthetically constructed.
Suppose a debtor owes $100 million in a floating-rate loan which he transacted, some time ago, at a rate of LIBOR +60 basis points. The debtor has put aside a lump sum amount of $8 million for interest expense for the remaining years of the loan’s life (say two years). Relating the $8 million to the loan amount $100 million implies an interest rate of 8% (i.e., $8 million/$100 million). It follows that the implied LIBOR level is 7.4% (i.e., 8%- 0.60%). However, LIBOR is currently trading at 7.2%, which means the debtor is still on the safe side of the trade. However, the expected rise in interest rates would turn things upside down, just if it occurred. The debtor enters the swap market so that he can lock in his interest expense. Assume he succeeded in doing a two year swap at 7.30% against LIBOR. Therefore, the effective rate on the loan would be:
Effective rate = swap rate + spread = 7.30% + 0.6% = 7.90%
| Interest | (LIBOR + 60) |
| Swap floating rate | LIBOR |
| Swap fixed rate | (7.30%) |
| Effective rate | (7.90%) |
The two floating rates (the one the debtor pays on the debt and the one he receives from the swap) cancel each other out leaving the debtor with a fixed rate that would help stabilize his interest payments in an environment of upward moving rates. Of course, the life of the swap should be equal to the remaining life of the debt under conversion.
Thanks to the swap, the debtor can ensure that his interest payments would be capped at a level lower than the rate implied from his budget. To be precise, the debtor is able to cut interest costs by:
Cost savings (%) = budget implied rate – effective rate= 8%- 7.90%
The swap didn’t only help fix interest expenses, but it also brought in cost savings to the tune of ten basis points (in absolute terms, this amounts to:
Cost savings = $100 million × 0.1% = $100,000




