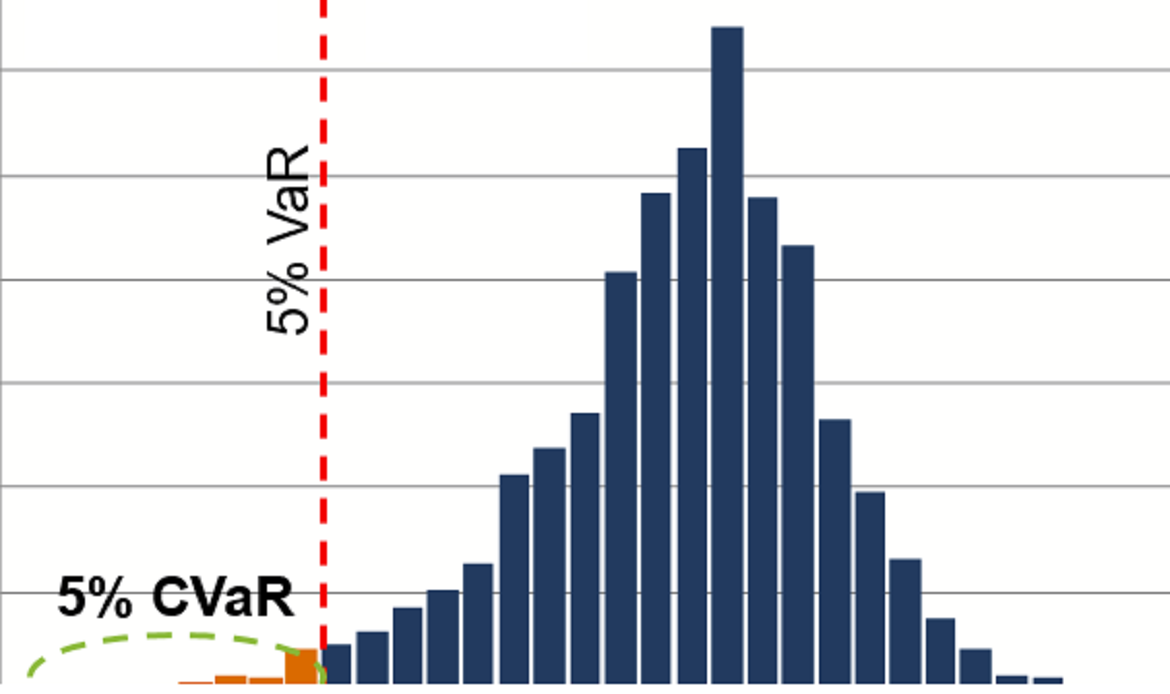
A method of calculating conditional value at risk (conditional VaR , CVaR) that modifies or expands it (the conditional VaR) to correct for skewness and flat tails in a portfolio’s returns. In other words, modified conditional VaR adjusts the normal measure of value at risk to account for non-normally distributed returns of specific asset classes (e.g., private equity, hedge funds or technology stocks, emerging market stocks, etc.)

In so doing, it takes the higher moments of the return distribution into account by extending the percentile of the standard normal distribution (using Cornish-Fisher extension). A portfolio can be optimized by minimizing the modified conditional value-at-risk at a given confidence level. Contrary to the normal value at risk, for a financial asset has negative skewness and/ or a positive excess kurtosis, the modified CVaR will be larger. Furthermore, the risk measured only using volatility will be lower than the risk measured using skewness, volatility and kurtosis.

For example, in view of the overall risk-averse against extreme negative returns, optimizing a portfolio using a modified VaR at 99% confidence level will result in the lowest probability of loss exceeding the modified CVaR at that confidence level.

This measure of risk is known for short as mCVaR (MCVaR).