A second-order greek that measures the instantaneous rate of change of an option’s delta with respect to the passage of time. In other words, it is the second-order derivative of the option value, once to the underlying price and once to the time decay. DdelT (also charm) is given by the following formula:

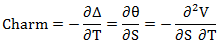
Charm may also be calculated as the derivative of theta with respect to the underlying’s price. As time passes, the option loses more of its time value (optionality), out-of-the-money options see their delta approach zero and in-the-money options see their delta become closer to that of an equivalent position in the underlying. In other words, call deltas approach one, whilst put deltas approach negative one.

The charm of a call option is calculated using the following expression:

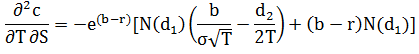
Where b is a generalized cost of carry factor.

The charm of a put option is given by:

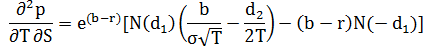
In order to arrive at the delta decay per day, this expression is usually divided by the number of days per year. Daily delta decay values can be fairly reliable when the number of days to expiration is sufficiently large. As an option approaches expiration, delta decay may accelerate to an extent that its day estimates become inaccurate.

DdelT or charm is also known as delta bleed (delta decay).